L'instrument principal du géomètre antique révélé par un papyrus

Publié le mardi 1^er Avril 2008.

La découverte inopinée d'un papyrus ptolémaïque permet d'élucider l'énigme du dodécaèdre, cet étrange objet que l'on rencontre assez fréquemment dans les fouilles gallo-romaines. Le dodécaèdre que nous présentons a été découvert en 2007 lors des fouilles de Cutry, en Meurthe-et-Moselle. Comme nous l'avions déjà indiqué dans un entrefilet, les archéologues dégagent peu à peu ce qui semble être une ville romaine d'une certaine importance en territoire trévire.

Ce type d'objet est connu par ailleurs1. On peut le décrire brièvement comme un polyèdre régulier2 dont les douze faces sont des pentagones, d'où le nom de dodécaèdre que les archéologues lui ont donné3. L‘objet est creux, et en bronze. Les faces sont percées d'un cercle, centré et d'un diamètre toujours différent, que ceignent des cercles gravés. A chaque sommet se dresse un ergot. Les dodécaèdres que l'on a découverts sont de tailles diverses mais tous tiennent dans le creux de la main ; celui que nous présentons fait 9,3 cm de large.

Ces objets sont longtemps restés un mystère pour les savants, qui ont émis plusieurs hypothèses quant leur utilisation : objet d'art, instrument pédagogique pour enseigner la géométrie aux élèves, chef-d'oeuvre d'un artisan amateur des théories mathématiques de l'époque, outil de géomètre... Or on a récemment démonté des sarcophages en cartonnage découverts dans une nécropole d'Alexandrie. L'un des papyrus récupérés lève le voile de l'énigme en expliquant comment fonctionnait cet instrument. Ce que certains pressentaient se trouve ainsi confirmé. Les papyrologues à l'origine de cette trouvaille nous ont permis d'étudier le document et de prendre des notes mais nous n'avons pas eu l'autorisation d'en faire une reproduction4. Le papyrus se présente comme un manuel et donne force détails sur le maniement de l'objet, sans rien dire toutefois de l'usage qu'on en faisait. Nous proposons cependant quelques hypothèses en fin d'article.Le dodécaèdre se posait sur deux ergots, et non sur une face comme on le supposait. Ils s'engageaient dans une embase, qui reposait sur un trépied. Les croquis du manuel montrent que les branches du trépied formaient un triangle équilatéral inscrit dans un cercle de trois pieds de rayon. Un fil à plomb suspendu au centre de l'embase pointait sur le centre du cercle. De cette manière on s'assurait de l'horizontalité de l'embase et de la hauteur du dodécaèdre. Bien qu'on ne puisse affirmer que ce triangle soit essentiel, nous pensons qu'il représente plus qu'un simple procédé d'installation. Autrement, en effet, celle-ci pourrait se révéler fort difficile.

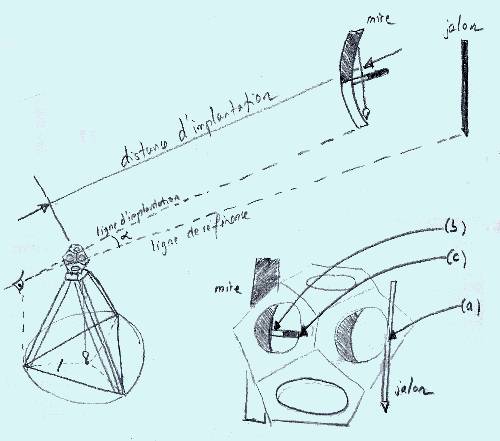
Une mire était associée au dodécaèdre, constituée d'une planche courbée dont la corde devait mesurer 6 pieds de haut. Le côté dirigé vers le dodécaèdre était séparé en deux parties égales ; la partie supérieure était peinte en rouge. Une planche de 3 pieds de long, fixée perpendiculairement à mi-hauteur, et dont la largeur était deux fois moindre que la partie verticale, était elle même divisée en deux parties d'égale longueur. A l'arrière de la mire, un fil à plomb, accroché à la partie supérieure, servait au porte-mire à s'assurer que sa mire était parfaitement verticale. Comme le trépied, l'embase, et éventuellement le socle triangulaire, devaient être en bois car seul l'instrument de bronze nous est parvenu. Si le socle était en bois, il devait être posé à l'horizontale, ce qui devait nécessiter un réglage particulièrement fin.L'opérateur se plaçait à l'arrière du dodécaèdre et visait un jalon sur la base de référence (a). Le porte mire se déplaçait à partir de cette ligne de référence jusqu'à ce que sa mire soit en limite du cercle (b). L'angle était ainsi facile à obtenir, mais des instruments bien plus simples auraient aisément rendu le même service. Ce qui en distinguait le dodécaèdre, c'était qu'il permettait de donner des distances. Le porte-mire se déplaçait en avant ou en arrière jusqu'à que la planche horizontale soit tangente aux cercles (b) ou (c). La moitié de la distance étant obtenue en visant la tangente de la moitié de la planche horizontale.Les rainures en cercles concentriques que l'on peut voir sur les faces du dodécaèdre étaient peintes de différentes couleurs. Un examen attentif a permis en effet de détecter des traces de pigments encore piégés dans les interstices. Le code de couleurs était associé à une table de conversion. Soixante combinaisons permettaient d'obtenir 60 distances et 60 angles différents. Ceux-ci étaient compris entre 30/Pi et 210/Pi (cette dernière mesure d'angle équivaut à environ 67°). Pour les distances, nous avons demandé à un mathématicien de nous établir une table de conversion car cela dépasse nos compétences en la matière. De manière très approximative, nous avons tablé sur des distances comprises entre 30 et 50 mètres avec une précision absolue de + ou – 15 centimètres. L'opérateur était placé à la verticale du cercle qui inscrit le socle triangulaire. En se plaçant à une distance deux fois moindre, on pouvait par exemple obtenir des angles supérieurs à 210/Pi ; au contraire, à une distance deux fois supérieure, on aurait pu implanter des points à 100 mètres environ, mais nous pensons que la précision en serait fortement affectée. Il est vraisemblable que l'on se soit contenté de cette dernière technique pour des implantations grossières mais on ne saurait le vérifier ni l'affirmer.Le même instrument pouvait servir à définir des pentes en utilisant les cercles verticaux. Nous proposons comme hypothèse qu'il a servi à établir le tracé de canaux d'irrigation et de grands axes routiers. On ne sera donc pas surpris de le rencontrer dans le contexte de l'urbanisation d'une agglomération romaine, comme à Cutry. Toutefois, l'emploi du dodécaèdre pour la route qui menait au palais d'Eumène II à Pergame5 reste sans conteste la plus surprenante. Dans le cadre de ses entreprises d'urbanisme monumental, le roi devait tenir compte du relief accidenté de la ville6 : aussi cette voie fut-elle construite selon une perspective faussée de sorte que, s'élargissant à mesure que l'on approchait du palais, elle donnât l'impression que la distance s'accroissait pourtant7.

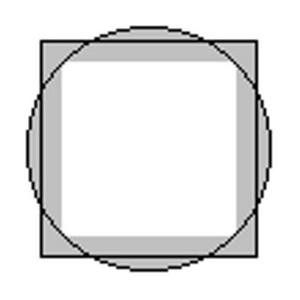
L'élargissement de la voie était calculée à l'aide d'une formule mathématique. Cette dernière donne le rapport entre le rayon d'un cercle et le côté d'un carré de surface équivalente avec une précision correcte. Ce problème de mathématiques fait partie des trois grands problèmes de l'Antiquité classique, la quadrature du cercle.

Ainsi, pour un observateur d'une taille de 1,60 m, la longueur supposée de la voie était de 100 m, alors que la réalité atteignait 672 m. La perspective inverse, dite accélérée, donnait une distance supposée d'environ 3000 m8.

L'édifice en devenait plus majestueux encore car cette perspective inversée le faisait paraître de plus en plus vaste. Cet artifice ne laissait pas de dérouter le visiteur et le livrait, au terme d'une approche oppressante mais pleine de prestige, à la volonté du roi et de ses administrateurs.

L'exemple d'Eumène II donne à penser que souverains et puissants considérèrent l'utilisation du dodécaèdre comme un moyen d'exprimer leurs desseins de magnificence. A l'époque impériale, l'autorité du Prince s'affirme par le biais de son administration. Les agrimensores, arpenteurs que les empereurs romains avaient constitués en collège et qu'ils rétribuaient sur les deniers de l'Etat, disposaient d'un pouvoir décisionnel immense. En établissant canaux, aqueducs, voies et rues, ils imprimaient au paysage l'empreinte de Rome. Ils décidaient ainsi de la vie des gens, mais aussi du fonctionnement de la société et du commerce. Grâce à eux s'imposait l'image de la toute-puissance de l'Empereur. Au fil du temps, le dodécaèdre devint le symbole de la mainmise du gouvernant sur le monde. Jusqu'à représenter la monarchie elle-même et orner le sceptre que brandit le souverain, ainsi que le révèle une enluminure sur un édit royal du XVe siècle conservé au musée de St Jean d'Acre.

• 1. On en trouve une bonne vingtaine dans les collections de divers musées, notamment au Musée Archéologique de Strasbourg et à la Saalburg, qui en possède plusieurs. Dans ces deux cas, il s'agit de camps militaires. Il n'est pas certain que la relation avec le monde militaire soit pertinente, mais cela mériterait d'être vérifié pour les autres exemplaires.
• 2. Le Larousse Universel donne pour polyèdre la définition suivante : solide limité de toutes parts par des plans. Ces plans, en se limitant mutuellement, constituent les faces du polyèdre. Les intersections en sont les arêtes et les points de rencontre de ces intersections sont les sommets. (...) Un polyèdre est dit régulier lorsque toutes ses faces sont des polygones réguliers égaux et que tous les angles dièdres sont égaux.
• 3. Dans le Larousse Universel, on lit pour dodécaèdre la définition suivante : n. m. (du gr. dodeka, douze, et edra, face). Géom. solide régulier terminé par douze pentagones égaux.
• 4. Cela fera en effet l'objet d'une publication dans la prestigieuse revue Alexandria publiée par l'Institut d'Archéologie du Caire.
• 5. Eumène II régna sur Pergame de 195 à 159 av. J.-C. L'amitié qu'il entretint avec Rome lui conféra une puissance sans rivale dans la région. Il protégea les arts et embellit sa capitale de monuments prestigieux.
• 6. L'application malheureuse du plan hippodamien au terrain montagneux de la nouvelle Priène était encore dans toutes les mémoires.
• 7. Vous trouverez sur Wikipédia un article très intéressant sur une perspective architecturale dite accélérée
• 8. Comme il est dit et prouvé au titre loi de Poisson, qui peut être utilisée en tant qu'approximation d'une loi binômiale B(n,p) lorsque n est "grand" et p "petit" (n > 50, p 0,1 et np 10), on a alors l = np.